How to Tell if a Curve Is Conservative

So since the two partial derivatives are not the same this vector field is NOT conservative. All of these checks are same in graph terms and in pixel terms.

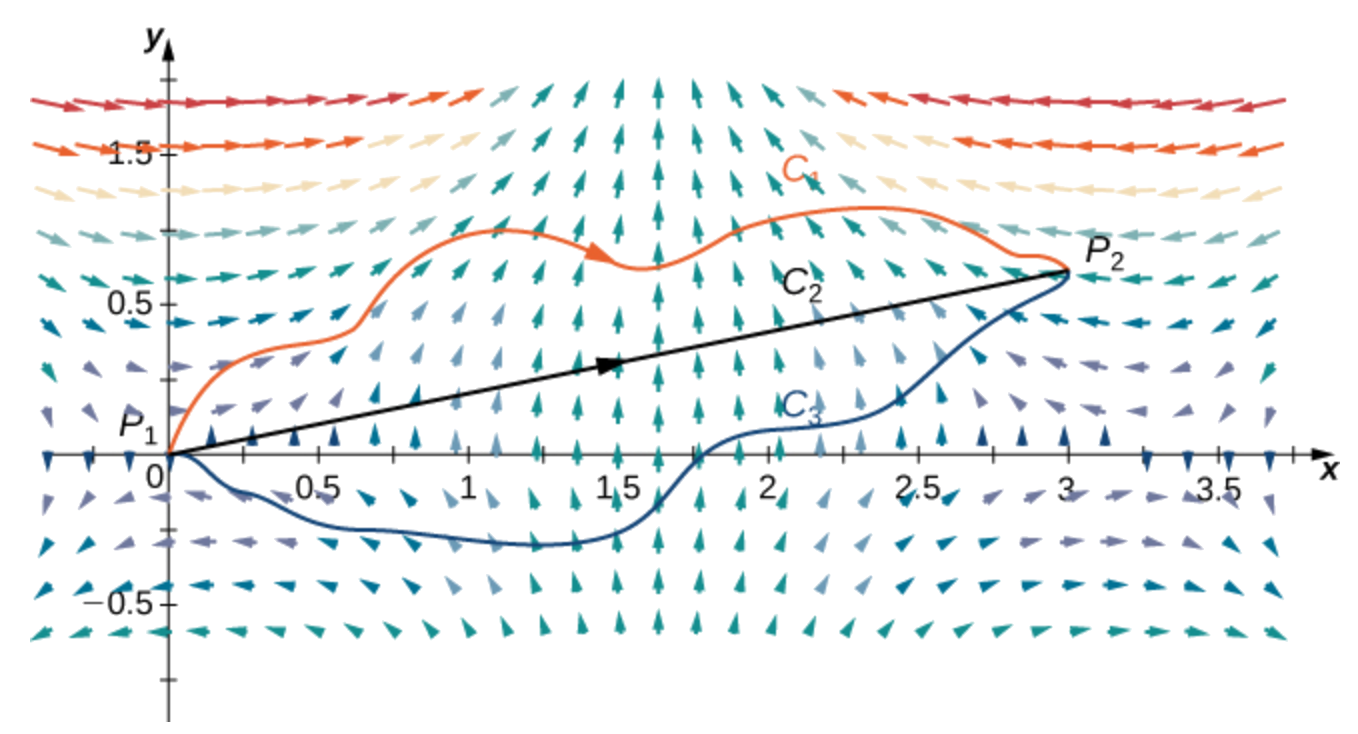
16 3 Conservative Vector Fields Mathematics Libretexts

In general the work done by a conservative vector field is zero along any closed curve.

. Notice that the curve begins and ends at the same place. Although this are all correct I dont think they are very clarifying. A vector field is called a conservative vector field if it satisfies any one of the following three properties all of which are defined within the article.

Line integrals of over closed loops are always. Since C is a closed curve the terminal point r b of C is the same as the initial point r. W closed path E consdr 0.

W closed path E cons d r 0. We do not even need to find the potential function since whatever it is say f we have fA - fA 0. Define problem in graph terms is only more clear.

Since the vector field is conservative we can use the fundamental theorem of line integrals. Answer 1 of 13. 1 find a potential function antiderivative for F and 2 compute the value of at the endpoints of C and calculate their.

In this section we develop conservative confidence intervals for the population percentage based on the sample percentage using Chebychevs Inequality and an upper bound on the SD of lists that contain only the numbers 0 and 1. Before we sketch the graph of the parametric curve recall that all parametric curves have a direction of motion ie. Line integrals of are path independent.

D R3 be a continuously differentiable vector field with domain D. If you see this f dot dr and someone asks you to evaluate this given that f is conservative or given that f is the gradient of another function or given that f is path independent you can now immediately say that is going to be equal to 0 which simplifies the. If a conservative vector field contains the entire curve C C C then the line integral over the curve C C C will be independent of path because every line integral in a conservative vector field is independent of path since all conservative vector fields are path independent.

Conservative vector fields are irrotational which means that the field has zero curl everywhere. Equivalently a force is conservative if the work it does around any closed path is zero. To check is curve closed or which type it is you have to check connectivity simplicity 2 neighbours andor self-intersection more neighbours.

We know that if F is a conservative vector field there are potential functions such that Therefore In other words just as with the Fundamental Theorem of Calculus computing the line integral where F is conservative is a two-step process. Divergence is an operation on a vector field that tells us how the field behaves toward or away from a point. To see why this is true let f be a potential function for F.

The first consequence is that if F is conservative and C is a closed curve then the circulation of F along C is zerothat is CF dr 0. If F is conservative then it satisfies curlF 0. 1 find a potential function antiderivative f.

For F and 2 compute the value of f. To know if a vector field F is conservative the first thing to check is the following criterion. So thats the neat take away here that if you know that this is conservative if you ever see something like this.

The direction indicating increasing values of the parameter t in this case. Is the gradient of some scalar-valued function ie. To determine if it is conservative you can find the actual function u such that.

Let D R3 be an open subset and let F. W ℓ F d x 0. In other words just as with the Fundamental Theorem of Calculus computing the line integral CF dr where F is conservative is a two-step process.

Locally the divergence of a vector field F in or at a particular point P is a measure of the outflowing-ness of the vector field at PIf F represents the velocity of a fluid then the divergence of F at P measures the net rate of change with respect to time of the. Conservative means that the chance that the procedure produces an interval that contains the population percentage is at least large as claimed. It says that a force field F xyz is conservative if and only if there exists a function φ xyz such that.

Show activity on this post. Because the curl of a gradient is 0 we can therefore express a conservative field. In previous problems one method we looked at was to build a table of values for a sampling of ts in the range provided.

In this case here is P P and Q Q and the appropriate partial derivatives. Therefore by comparison These above three equations are satisfied by. For example the force field due to gravity acting on a body of mass m is equal to where we define gravity as pointing in the negative z -direction.

We are able to calculate that the curl of a gradient is zero curl nabla f vc 0 for any twice repeatedly differentiable f. This equation means that the total kinetic and potential energy is constant for any process involving only conservative forces. 3 hours agoBut as of last week the majority of five justices to strike Roe remains intact according to three conservatives close to the court who like others spoke on the condition of anonymity to discuss a sensitive matter.

That is conservative forces onlyKEPE constant or KEi PEi KEf PEf conservative forces only KE PE constant or KE i PE i KE f PE f where i and f denote initial and final values. This situation relies on the truth that a vector discipline dlvf is conservative if and provided that dlvf nabla f for some potential operate. P x 2 y x P y x Q y 2 x y Q x y P x 2 y x P y x Q y 2 x y Q x y.

Independence of path is a property of conservative vector fields. For some function. There has been a couple of answers that state that by definition a conservative field is that which can be written as the gradient of a scalar function or directly that whose curl is zero.

Ill try to explai. At the endpoints of C. It is same to look on it as graph or pixel problem.

Explicitly F F 1F2F3 satisfies the three conditions. A person close to the most conservative members of the court said Roberts told his fellow jurists in a private conference in. If it is conservative then vec F nabla phi for some potential phi using a very useful identity nabla times vec F nabla times nablaphi 0 this mean that if the field is conservative it wont curl around any point it will be straight lines something that looks like electric or gravitationnal field.

If t is time then the force does not depend on the position then all the derivatives are zero and its trivial to say that F 0. But a sufficiency test is to take the cross partial derivatives. If a force is perpendicular to the motion then F x 0 t then the work.

Line Integrals Is This Vector Field Conservative My Team Thinks It Is Conservative I Don T Mathematics Stack Exchange

Calculus 3 Line Integrals 38 Of 44 What Are Conservative Non Conservative Vector Fields Youtube

Stokes Theorem Resolved Nonsense Circulation In A Conservative Vector Field Mathematics Stack Exchange

Calculus 3 Line Integrals 38 Of 44 What Are Conservative Non Conservative Vector Fields Youtube